publications

2025

1. Symmetric Algebraic Circuits and Homomorphism Polynomials

   Anuj Dawar, Benedikt Pago, and Tim Seppelt

   Feb 2025

   Abstract arXiv

   The central open question of algebraic complexity is whether VP is unequal to VNP, which is saying that the permanent cannot be represented by families of polynomial-size algebraic circuits. For symmetric algebraic circuits, this has been confirmed by Dawar and Wilsenach (2020) who showed exponential lower bounds on the size of symmetric circuits for the permanent. In this work, we set out to develop a more general symmetric algebraic complexity theory. Our main result is that a family of symmetric polynomials admits small symmetric circuits if and only if they can be written as a linear combination of homomorphism counting polynomials of graphs of bounded treewidth. We also establish a relationship between the symmetric complexity of subgraph counting polynomials and the vertex cover number of the pattern graph. As a concrete example, we examine the symmetric complexity of immanant families (a generalisation of the determinant and permanent) and show that a known conditional dichotomy due to Curticapean (2021) holds unconditionally in the symmetric setting.

2024

1. NPA Hierarchy for Quantum Isomorphism and Homomorphism Indistinguishability

   Prem Nigam Kar, David E. Roberson, Tim Seppelt, and Peter Zeman

   Jul 2024

   Abstract arXiv

   Mančinska and Roberson [FOCS’20] showed that two graphs are quantum isomorphic if and only if they are homomorphism indistinguishable over the class of planar graphs. Atserias et al. [JCTB’19] proved that quantum isomorphism is undecidable in general. The NPA hierarchy gives a sequence of semidefinite programming relaxations of quantum isomorphism. Recently, Roberson and Seppelt [ICALP’23] obtained a homomorphism indistinguishability characterization of the feasibility of each level of the Lasserre hierarchy of semidefinite programming relaxations of graph isomorphism. We prove a quantum analogue of this result by showing that each level of the NPA hierarchy of SDP relaxations for quantum isomorphism of graphs is equivalent to homomorphism indistinguishability over an appropriate class of planar graphs. By combining the convergence of the NPA hierarchy with the fact that the union of these graph classes is the set of all planar graphs, we are able to give a new proof of the result of Mančinska and Roberson [FOCS’20] that avoids the use of the theory of quantum groups. This homomorphism indistinguishability characterization also allows us to give a randomized polynomial-time algorithm deciding exact feasibility of each fixed level of the NPA hierarchy of SDP relaxations for quantum isomorphism.

2024

1. 

   An Algorithmic Meta Theorem for Homomorphism Indistinguishability

   Tim Seppelt

   In 49th International Symposium on Mathematical Foundations of Computer Science (MFCS 2024), Aug 2024

   Abstract arXiv URL DOI Slides

   Two graphs G and H are homomorphism indistinguishable over a class of graphs 𝓕 if for all graphs F ∊ 𝓕 the number of homomorphisms from F to G is equal to the number of homomorphisms from F to H. Many natural equivalence relations comparing graphs such as (quantum) isomorphism, spectral, and logical equivalences can be characterised as homomorphism indistinguishability relations over certain graph classes.
   For a fixed graph class 𝓕, the decision problem HomInd(𝓕) asks to determine whether two input graphs G and H are homomorphism indistinguishable over 𝓕. The problem HomInd(𝓕) is known to be decidable only for few graph classes F. We show that HomInd(𝓕) admits a randomised polynomial-time algorithm for every graph class 𝓕 of bounded treewidth which is definable in counting monadic second-order logic CMSO2. Thereby, we give the first general algorithm for deciding homomorphism indistinguishability.
   This result extends to a version of HomInd where the graph class 𝓕 is specified by a CMSO2-sentence and a bound k on the treewidth, which are given as input. For fixed k, this problem is randomised fixed-parameter tractable. If k is part of the input then it is coNP- and coW[1]-hard. Addressing a problem posed by Berkholz (2012), we show coNP-hardness by establishing that deciding indistinguishability under the k-dimensional Weisfeiler–Leman algorithm is coNP-hard when k is part of the input.

2. 

   The Complexity of Homomorphism Reconstructibility

   Jan Böker, Louis Härtel, Nina Runde, Tim Seppelt, and Christoph Standke

   In 41st International Symposium on Theoretical Aspects of Computer Science (STACS 2024), Mar 2024

   Abstract arXiv URL DOI

   Representing graphs by their homomorphism counts has led to the beautiful theory of homomorphism indistinguishability in recent years. Moreover, homomorphism counts have promising applications in database theory and machine learning, where one would like to answer queries or classify graphs solely based on the representation of a graph G as a finite vector of homomorphism counts from some fixed finite set of graphs to G. We study the computational complexity of the arguably most fundamental computational problem associated to these representations, the homomorphism reconstructability problem: given a finite sequence of graphs and a corresponding vector of natural numbers, decide whether there exists a graph G that realises the given vector as the homomorphism counts from the given graphs.
   We show that this problem yields a natural example of an NP^#P-hard problem, which still can be NP-hard when restricted to a fixed number of input graphs of bounded treewidth and a fixed input vector of natural numbers, or alternatively, when restricted to a finite input set of graphs. We further show that, when restricted to a finite input set of graphs and given an upper bound on the order of the graph G as additional input, the problem cannot be NP-hard unless P=NP. For this regime, we obtain partial positive results. We also investigate the problem’s parameterised complexity and provide fpt-algorithms for the case that a single graph is given and that multiple graphs of the same order with subgraph instead of homomorphism counts are given.

3. 

   Going Deep and Going Wide: Counting Logic and Homomorphism Indistinguishability over Graphs of Bounded Treedepth and Treewidth

   Eva Fluck, Tim Seppelt, and Gian Luca Spitzer

   In 32nd EACSL Annual Conference on Computer Science Logic (CSL 2024), Feb 2024

   Abstract arXiv URL DOI

   We study the expressive power of first-order logic with counting quantifiers, especially the k-variable and quantifier-rank-q fragment 𝖢^k_q, using homomorphism indistinguishability. Recently, Dawar, Jakl, and Reggio (2021) proved that two graphs satisfy the same 𝖢^k_q-sentences if and only if they are homomorphism indistinguishable over the class 𝒯^k_q of graphs admitting a k-pebble forest cover of depth q. Their proof builds on the categorical framework of game comonads developed by Abramsky, Dawar, and Wang (2017). We reprove their result using elementary techniques inspired by Dvořák (2010). Using these techniques we also give a characterisation of guarded counting logic. Our main focus, however, is to provide a graph theoretic analysis of the graph class 𝒯^k_q. This allows us to separate 𝒯^k_q from the intersection of the graph class TW_k-1, that is graphs of treewidth less or equal k-1, and TD_q, that is graphs of treedepth at most q if q is sufficiently larger than k. We are able to lift this separation to the semantic separation of the respective homomorphism indistinguishability relations. A part of this separation is to prove that the class TD_q is homomorphism distinguishing closed, which was already conjectured by Roberson (2022).

4. 

   Limitations of Game Comonads for Invertible-Map Equivalence via Homomorphism Indistinguishability

   Moritz Lichter, Benedikt Pago, and Tim Seppelt

   In 32nd EACSL Annual Conference on Computer Science Logic (CSL 2024), Feb 2024

   Abstract arXiv URL DOI

   Abramsky, Dawar, and Wang (2017) introduced the pebbling comonad for k-variable counting logic and thereby initiated a line of work that imports category theoretic machinery to finite model theory. Such game comonads have been developed for various logics, yielding characterisations of logical equivalences in terms of isomorphisms in the associated co-Kleisli category. We show a first limitation of this approach by studying linear-algebraic logic, which is strictly more expressive than first-order counting logic and whose k-variable logical equivalence relations are known as invertible-map equivalences (IM). We show that there exists no finite-rank comonad on the category of graphs whose co-Kleisli isomorphisms characterise IM-equivalence, answering a question of Ó Conghaile and Dawar (CSL 2021). We obtain this result by ruling out a characterisation of IM-equivalence in terms of homomorphism indistinguishability and employing the Lovász-type theorem for game comonads established by Reggio (2022). Two graphs are homomorphism indistinguishable over a graph class if they admit the same number of homomorphisms from every graph in the class. The IM-equivalences cannot be characterised in this way, neither when counting homomorphisms in the natural numbers, nor in any finite prime field.

2023

1. 

   Logical Equivalences, Homomorphism Indistinguishability, and Forbidden Minors

   Tim Seppelt

   In 48th International Symposium on Mathematical Foundations of Computer Science (MFCS 2023), Aug 2023

   Abstract arXiv URL DOI Slides

   Two graphs G and H are homomorphism indistinguishable over a class of graphs 𝓕 if for all graphs F ∊ 𝓕 the number of homomorphisms from F to G is equal to the number of homomorphisms from F to H. Many natural equivalence relations comparing graphs such as (quantum) isomorphism, spectral, and logical equivalences can be characterised as homomorphism indistinguishability relations over certain graph classes.
   Abstracting from the wealth of such instances, we show in this paper that equivalences w.r.t. any self-complementarity logic admitting a characterisation as homomorphism indistinguishability relation can be characterised by homomorphism indistinguishability over a minor-closed graph class. Self-complementarity is a mild property satisfied by most well-studied logics. This result follows from a correspondence between closure properties of a graph class and preservation properties of its homomorphism indistinguishability relation.
   Furthermore, we classify all graph classes which are in a sense finite (essentially profinite) and satisfy the maximality condition of being homomorphism distinguishing closed, i.e. adding any graph to the class strictly refines its homomorphism indistinguishability relation. Thereby, we answer various questions raised by Roberson (2022) on general properties of the homomorphism distinguishing closure.

2. 

   Lasserre Hierarchy for Graph Isomorphism and Homomorphism Indistinguishability

   David E. Roberson, and Tim Seppelt

   In 50th International Colloquium on Automata, Languages, and Programming (ICALP 2023), Jul 2023

   Abstract arXiv URL DOI Slides

   We show that feasibility of the t^th level of the Lasserre semidefinite programming hierarchy for graph isomorphism can be expressed as a homomorphism indistinguishability relation. In other words, we define a class ℒ_t of graphs such that graphs G and H are not distinguished by the t^th level of the Lasserre hierarchy if and only if they admit the same number of homomorphisms from any graph in ℒ_t. By analysing the treewidth of graphs in ℒ_t we prove that the 3t^th level of Sherali-Adams linear programming hierarchy is as strong as the t^th level of Lasserre. Moreover, we show that this is best possible in the sense that 3t cannot be lowered to 3t-1 for any t. The same result holds for the Lasserre hierarchy with non-negativity constraints, which we similarly characterise in terms of homomorphism indistinguishability over a family ℒ_t^+ of graphs. Additionally, we give characterisations of level-t Lasserre with non-negativity constraints in terms of logical equivalence and via a graph colouring algorithm akin to the Weisfeiler-Leman algorithm. This provides a polynomial time algorithm for determining if two given graphs are distinguished by the t^th level of the Lasserre hierarchy with non-negativity constraints.

3. 

   Weisfeiler-Leman and Graph Spectra

   Gaurav Rattan, and Tim Seppelt

   In Proceedings of the 2023 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), Feb 2023

   Abstract arXiv URL DOI Slides

   Two simple undirected graphs are cospectral if their respective adjacency matrices have the same multiset of eigenvalues. Cospectrality yields an equivalence relation on the family of graphs which is provably weaker than isomorphism. In this paper, we study cospectrality in relation to another well-studied relaxation of isomorphism, namely k-dimensional Weisfeiler-Leman (k-WL) indistinguishability. Cospectrality with respect to standard graph matrices such as the adjacency or the Laplacian matrix yields a strictly finer equivalence relation than 2-WL indistinguishability. We show that individualising one vertex plus running 1-WL already subsumes cospectrality with respect to all such graph matrices. Building on this result, we resolve an open problem of Fürer (2010) about spectral invariants.
   Looking beyond 2-WL, we devise a hierarchy of graph matrices generalising the adjacency matrix such that k-WL indistinguishability after a fixed number of iterations can be captured as a spectral condition on these matrices. Precisely, we provide a spectral characterisation of k-WL indistinguishability after d iterations, for k,d ∈ ℕ. Our results can be viewed as characterisations of homomorphism indistinguishability over certain graph classes in terms of matrix equations. The study of homomorphism indistinguishability is an emerging field, to which we contribute by extending the algebraic framework of Mančinska and Roberson (2020) and Grohe et al. (2022).

2022

1. 

   Homomorphism Tensors and Linear Equations

   Martin Grohe, Gaurav Rattan, and Tim Seppelt

   In 49th International Colloquium on Automata, Languages, and Programming (ICALP 2022), Jul 2022

   Abstract arXiv URL DOI Poster Slides

   Lovász (1967) showed that two graphs G and H are isomorphic if and only if they are homomorphism indistinguishable over the class of all graphs, i.e. for every graph F, the number of homomorphisms from F to G equals the number of homomorphisms from F to H. Recently, homomorphism indistinguishability over restricted classes of graphs such as bounded treewidth, bounded treedepth and planar graphs, has emerged as a surprisingly powerful framework for capturing diverse equivalence relations on graphs arising from logical equivalence and algebraic equation systems.
   In this paper, we provide a unified algebraic framework for such results by examining the linear-algebraic and representation-theoretic structure of tensors counting homomorphisms from labelled graphs. The existence of certain linear transformations between such homomorphism tensor subspaces can be interpreted both as homomorphism indistinguishability over a graph class and as feasibility of an equational system. Following this framework, we obtain characterisations of homomorphism indistinguishability over several natural graph classes, namely trees of bounded degree, graphs of bounded pathwidth (answering a question of Dell et al. (2018)), and graphs of bounded treedepth.

2024

1. 

   Logical equivalences, homomorphism indistinguishability, and forbidden minors

   Tim Seppelt

   Information and Computation, Sep 2024

   Abstract arXiv URL DOI Slides

   Two graphs G and H are homomorphism indistinguishable over a class of graphs 𝓕 if for all graphs F ∊ 𝓕 the number of homomorphisms from F to G is equal to the number of homomorphisms from F to H. Many natural equivalence relations comparing graphs such as (quantum) isomorphism, spectral, and logical equivalences can be characterised as homomorphism indistinguishability relations over certain graph classes.
   Abstracting from the wealth of such instances, we show in this paper that equivalences w.r.t. any self-complementarity logic admitting a characterisation as homomorphism indistinguishability relation can be characterised by homomorphism indistinguishability over a minor-closed graph class. Self-complementarity is a mild property satisfied by most well-studied logics.
   Furthermore, we classify all graph classes which are in a sense finite (essentially profinite) and satisfy the maximality condition of being homomorphism distinguishing closed, i.e. adding any graph to the class strictly refines its homomorphism indistinguishability relation. Thereby, we answer various questions raised by Roberson (2022) on general properties of the homomorphism distinguishing closure.

2. 

   Lasserre Hierarchy for Graph Isomorphism and Homomorphism Indistinguishability

   David E. Roberson, and Tim Seppelt

   TheoretiCS, Sep 2024

   Abstract URL DOI Slides

   We show that feasibility of the t^th level of the Lasserre semidefinite programming hierarchy for graph isomorphism can be expressed as a homomorphism indistinguishability relation. In other words, we define a class ℒ_t of graphs such that graphs G and H are not distinguished by the t^th level of the Lasserre hierarchy if and only if they admit the same number of homomorphisms from any graph in ℒ_t. By analysing the treewidth of graphs in ℒ_t we prove that the 3t^th level of Sherali-Adams linear programming hierarchy is as strong as the t^th level of Lasserre. Moreover, we show that this is best possible in the sense that 3t cannot be lowered to 3t-1 for any t. The same result holds for the Lasserre hierarchy with non-negativity constraints, which we similarly characterise in terms of homomorphism indistinguishability over a family ℒ_t^+ of graphs. Additionally, we give characterisations of level-t Lasserre with non-negativity constraints in terms of logical equivalence and via a graph colouring algorithm akin to the Weisfeiler-Leman algorithm. This provides a polynomial time algorithm for determining if two given graphs are distinguished by the t^th level of the Lasserre hierarchy with non-negativity constraints.

2023

1. 

   Building blocks of polycentric governance

   Tiffany H. Morrison, Örjan Bodin, Graeme S. Cumming, Mark Lubell, Ralf Seppelt, Tim Seppelt, and Christopher M. Weible

   Policy Studies Journal, Jan 2023

   Abstract URL DOI

   Success or failure of a polycentric system is a function of complex political and social processes, such as coordination between actors and venues to solve specialized policy problems. Yet there is currently no accepted method for isolating distinct processes of coordination, nor to understand how their variance affects polycentric governance performance. We develop and test a building-blocks approach that uses different patterns or “motifs” for measuring and comparing coordination longitudinally on Australia’s Great Barrier Reef. Our approach confirms that polycentric governance comprises an evolving substrate of interdependent venues and actors over time. However, while issue specialization and actor participation can be improved through the mobilization of venues, such a strategy can also fragment overall polycentric capacity to resolve conflict and adapt to new problems. A building-blocks approach advances understanding and practice of polycentric governance by enabling sharper diagnosis of internal dynamics in complex environmental governance systems.

2024

1. 

   Homomorphism Indistinguishability

   Tim Seppelt

   Nov 2024

   PhD thesis

   Abstract PDF URL DOI Slides

   Two graphs G and H are homomorphism indistinguishable over a class of graphs 𝓕 if, for all graphs F ∊ 𝓕, the number of homomorphisms from F to G is equal to the number of homomorphisms from F to H. In 1967, Lovász showed that two graphs are isomorphic if, and only if, they are homomorphism indistinguishable over the class of all graphs. Subsequently, many graph isomorphism relaxations such as quantum isomorphism, spectral, and logical equivalences have been characterised as homomorphism indistinguishability relations over certain graph classes. Thereby, homomorphism indistinguishability connects seemingly disparate fields such as quantum information, finite model theory, and machine learning.

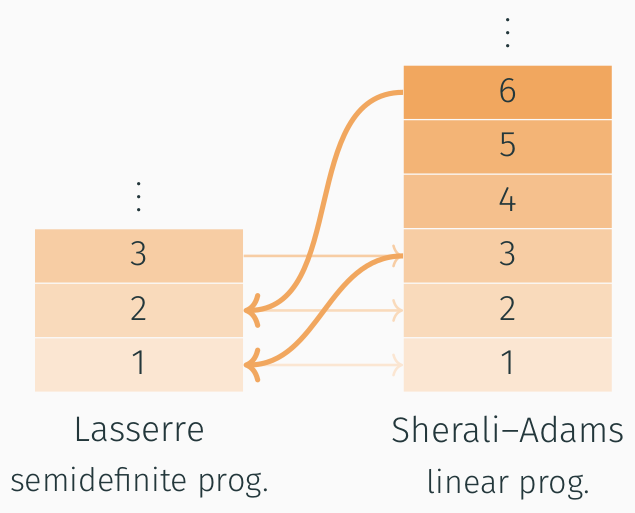
   This thesis explores three themes: We first review the plenitude of characterisations of graph isomorphism relaxations as a homomorphism indistinguishability relation. Focusing on integer programming relaxations for graph isomorphism, we prove that the feasibility of each level of the Sherali–Adams and Lasserre hierarchies is characterised as homomorphism indistinguishability relations. These results, which are derived using (bi)labelled graphs and homomorphism tensors, shed light on the distinguishing power of these hierarchies. In particular, we determine the precise number of Sherali–Adams levels necessary such that their feasibility guarantees the feasibility of a given Lasserre level.

   Abstracting from the wealth of homomorphism indistinguishability characterisations, we embark on a more principled study of homomorphism indistinguishability investigating the distinguishing power and the complexity of homomorphism indistinguishability relations over minor-closed graph class.

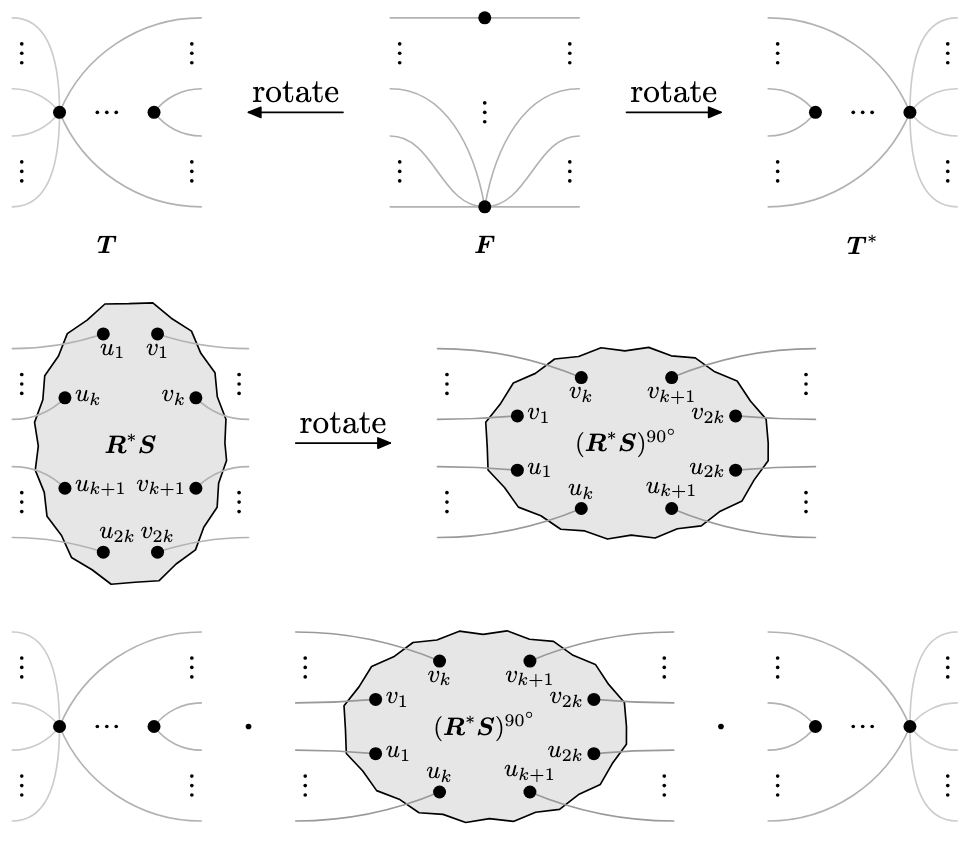
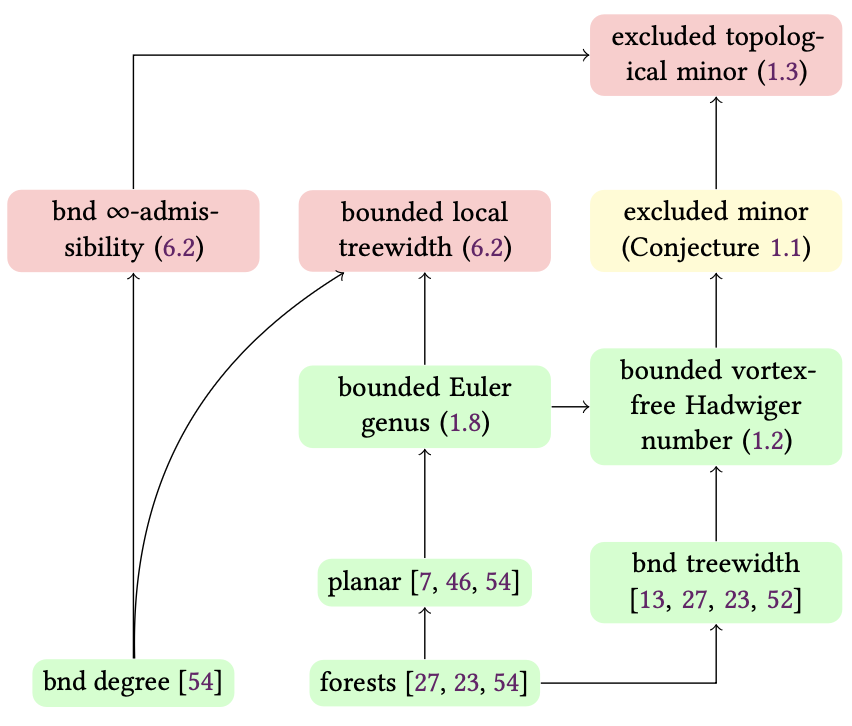
   The homomorphism distinguishing closure cl(𝓕) of a graph class 𝓕 is the central notion for studying the distinguishing power of homomorphism indistinguishability relations. It is defined as the maximal graph class whose homomorphism indistinguishability relation coincides with the one of 𝓕. Roberson conjectured that every minor-closed union-closed graph class 𝓕 is homomorphism distinguishing closed, i.e. cl(𝓕) = 𝓕. We confirm Roberson’s conjecture, which is generally wide open, for further graphs classes and prove unconditionally that if 𝓕 is minor-closed then so is cl(𝓕).

   Lastly, we investigate the complexity of deciding whether two graphs are homomorphism indistinguishable over a fixed graph class. For infinite graph classes, this problem is a priori not even decidable. In stark contrast to this, we show that, over every minor-closed graph class of bounded treewidth, homomorphism indistinguishability can be decided in randomised polynomial time.

2020

1. 

   motifr: Motif Analysis in Multi-Level Networks

   Mario Angst, and Tim Seppelt

   Nov 2020

   R package

   URL

2019

1. The Graph Isomorphism Problem: Local Certificates for Giant Action

   Tim Seppelt

   Sep 2019

   Bachelor’s thesis

   Abstract arXiv

   This thesis provides an explanation of L}’aszl}’o Babai’s quasi-polynomial algorithm for the Graph Isomorphism Problem published in 2015 with a particular focus on the case of local certificates, i.e. the case that cannot be dealt with by Luks’ method. The thesis extends the explanations provided by Harald Andr}’es Helfgott in 2017. It is concluded that the complexity of Babai’s algorithm is {}exp}left(C }left(}log n}right)^3}right) for \n the number of vertices, \C a constant. Group theoretical and combinatorial arguments are used to give more details on Babai’s method of local certificates. They treat Luks’ barrier case in which the imprimitve permutation group \G can be mapped onto an alternating group with large domain.